Flowchart

Diagram alir

Dari Wikipedia bahasa Indonesia, ensiklopedia bebas

Contoh diagram alir proses yang berhubungan dengan kerusakan lampu.

Contoh diagram alir untuk menghitung factorial N (N!)

Flowchart atau diagram alir merupakan sebuah diagram dengan simbol-simbol grafis yang menyatakan aliran algoritma atau prosesyang menampilkan langkah-langkah yang disimbolkan dalam bentuk kotak, beserta urutannya dengan menghubungkan masing masing langkah tersebut menggunakan tanda panah. Diagram ini bisa memberi solusi selangkah demi selangkah untuk penyelesaian masalah yang ada di dalam proses atau algoritma tersebut.^[1]

Pseudo-code

Kode palsu

Dari Wikipedia bahasa Indonesia, ensiklopedia bebas

Kode-palsu atau dalam bahasa inggris lebih dikenal sebagai pseudo-code merupakan deskripsi tingkat tinggi informal dan ringkas atas algoritma pemrograman komputer yang menggunakan konvensi struktural atas suatu bahasa pemrograman, dan ditujukan untuk dibaca oleh manusia dan bukan oleh mesin. Kode palsu biasanya tidak menggunakan elemen detail yang tidak diperlukan untuk kebutuhan pemahaman manusia atas suatu algoritma, seperti deklarasi variabel, kode ataupun subrutin untuk sistem yang bersifat spesifik. Bahasa pemrograman yang digunakan lebih diperbanyak dengan deskripsi dalam bahasa natural atas sesuatu hal yang bersifat detail, atau dengan menggunakan notasi matematis. Tujuan dari penggunaan kode-palsu adalah untuk mempermudah manusia dalam pemahaman dibandingkan menggunakan bahasa pemrograman yang umum digunakan, terlebih aspeknya yang ringkas serta tidak bergantung pada suatu sistem tertentu merupakan prinsip utama dalam suatu algoritma. Kode-palsu umumnya digunakan dalam buku-buku ataupun publikasi karya ilmiah yang mendokumentasikan suatu algortima, dan juga dalam perencanaan pengembangan program komputer, untuk membuat sketsa atas struktur sebuah program sebelum program yang sesungguhnya ditulis.

Algoritma

Dari Wikipedia bahasa Indonesia, ensiklopedia bebas

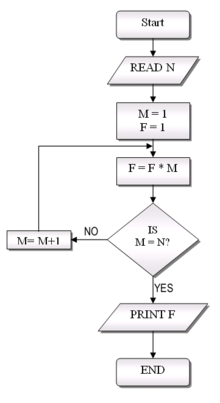
Diagram alur dari sebuah algoritma (Algoritma Euclid) untuk menghitung faktor persekutuan terbesar (f.p.k.) dari dua angka a dan b dalam lokasi bernama A dan B. Algoritma dijalankan dengan pengurangan berturut-turut dalam dua pengulangan: JIKA pengujian B >= A menghasilkan "ya" (atau benar) (lebih akuratnya angka bdalam lokasi B lebih besar atau sama dengan angka a dalam lokasi A) MAKA, algoritma menentukan B ← B - A (artinya angka b - a menggantikan bsebelumnya). Hal yang sama, JIKA A > B, MAKA A ← A - B. Proses tersebut berhenti saat (isi dari) B adalah 0, menghasilkan f.p.k. dalam A. (Algoritma tersebut diambil dari Scott 2009:13; simbol dan gaya penggambaran dari Tausworthe 1977).

Dalam matematika dan ilmu komputer, algoritma adalah prosedur langkah-demi-langkah untuk penghitungan. Algoritma digunakan untukpenghitungan, pemrosesan data, dan penalaran otomatis.

Algoritma adalah metode efektif diekspresikan sebagai rangkaian terbatas ^[1] dari instruksi-instruksi yang telah didefinisikan dengan baik^[2] untuk menghitung sebuah fungsi.^[3] Dimulai dari sebuah kondisi awal dan input awal (mungkin kosong),^[4] instruksi-instruksi tersebut menjelaskan sebuah komputasi yang, bila dieksekusi, diproses lewat sejumlah urutan kondisi terbatas ^[5] yang terdefinisi dengan baik, yang pada akhirnya menghasilkan "keluaran" ^[6] dan berhenti di kondisi akhir. Transisi dari satu kondisi ke kondisi selanjutnya tidak harusdeterministik; beberapa algoritma, dikenal dengan algoritma pengacakan, menggunakan masukan acak.^[7]

Walaupun algorism-nya al-Khawarizmi dirujuk sebagai aturan-aturan melakukan aritmetika menggunakan bilangan Hindu-Arab dan solusi sistematis dan persamaan kuadrat, sebagian formalisasi yang nantinya menjadi algoritma modern dimulai dengan usaha untuk memecahkan permasalahan keputusan (Entscheidungsproblem) yang diajukan oleh David Hilbert pada tahun 1928. Formalisasi selanjutnya dilihat sebagai usaha untuk menentukan "penghitungan efektif" ^[8] atau "metode efektif"; ^[9] formalisasi tersebut mengikutkanGodel-Herbrand-Kleene fungsi rekursif-nya Kurt Godel - Jacques Herbrand - Stephen Cole Kleene pada tahun 1930, 1934, dan 1935,kalkulus lambda-nya Alonzo Church pada tahun 1936, "Formulasi 1"-nya Emil Post pada tahun 1936, dan Mesin Turing-nya Alan Turingpada tahun 1936-7 dan 1939. Dari definisi formal dari algoritma di atas, berkaitan dengan konsep intuituf, masih tetap ada masalah yang menantang. ^[10]

15 Laptop Gaming Terbaik dengan Harga 5 Jutaan (Update 2016)

15 Laptop Gaming Murah 5 Jutaan

sumber : https://jalantikus.com/gadgets/laptopgamingmurah/utm_source=Desktop&utm_medium=Push&utm_campaign=JTPush

Laptop gaming harga murah 5 Jutaan yang JalanTikus rangkum dari beragai sumber berikut ini bisa digunakan untuk kebutuhan Low to Medium gaming. Jadi kamu jangan memaksakan laptop gaming terbaru 2016 berikut untuk memainkan beberapa game berat seperti:

• 
  
• GTA V
• Assasins Creed Unity
• Batman: Arkham Knight
• Ryse: Son of Rome
• Thief
• Crysis 3
• Dll

Berikut adalah referensi daftar harga laptop gaming murah harga 5 jutaan:

Hobby Downhill

kembali lagi dengan saya .... kali ini saya akan menceritakan hobby/hoby/hobi atau apalah itu.. downhill / naik sepeda menuruni bukit/gunung .

Perkenalan Singkat

Bissmillahhirohmannirohim ... 
Perkenalkan nama saya arif ramadha gunara .  saya tinggal di banjar , tepatnya di 
Jl.dewisartika RT06/08